über 170 kostenlose
Prüfungsaufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
AB SOFORT: KEIN LOGIN mehr erforderlich - alle Lösungen zu den Prüfungsaufgaben sind frei zugänglich.
 
Mittlere-Reife-Prüfung 2010 Mathematik I Aufgabe A2
Aufgabe A2.

Der Punkt A ( 0 | 0 ) ist gemeinsamer Eckpunkt von gleichschenkligen Dreiecken A B n C n , wobei die Punkte C n ( x | 1 2 x + 6 ) auf der Geraden g mit der Gleichung y = 1 2 x + 6 liegen ( 𝔾 = ℝ × ℝ ). Die Basiswinkel B n A C n und A C n B n der Dreiecke A B n C n haben das Maß 30 ∘ .


Aufgabe A2.1  (1 Punkt)

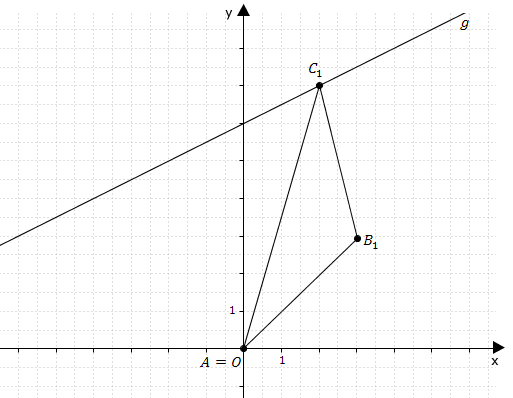
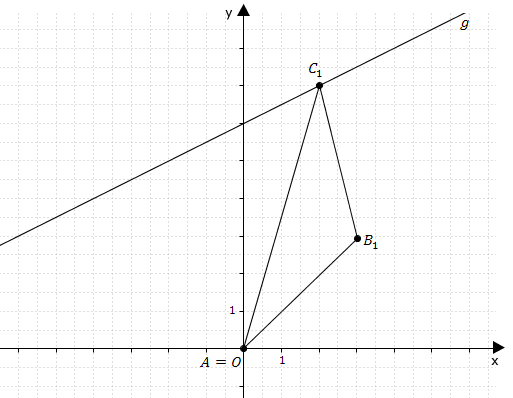
In das Koordinatensystem zu 2.0 ist das Dreieck A B 1 C 1 für x = 2 eingezeichnet. Zeichnen Sie das Dreieck A B 2 C 2 für x = - 3 ein.

Aufgabe A2.2  (3 Punkte)

Zeigen Sie, dass für das Längenverhältnis der Strecken [ A B n ] und [ A C n ] gilt:
A B n ¯ = 1 3 ⋅ A C n ¯ .
Bestätigen Sie sodann durch Rechnung, dass für den Flächeninhalt A der Dreiecke A B n C n in Abhängigkeit von der Abszisse x der Punkte C n gilt:
A ( x ) = 1 4 3 ⋅ ( 1 , 25 x 2 + 6 x + 36 ) FE

Aufgabe A2.3  (2 Punkte)

Unter den Dreiecken A B n C n hat das Dreieck A B 0 C 0 den minimalen Flächeninhalt.
Berechnen Sie die Koordinaten des Punktes C 0 .

Aufgabe A2.4  (3 Punkte)

Berechnen Sie die Koordinaten der Punkte B n in Abhängigkeit von der Abszisse x der Punkte C n . Runden Sie auf zwei Stellen nach dem Komma.

Lösung als Video:
video

 
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?